Enviar un artículo
issn

Factor de impacto
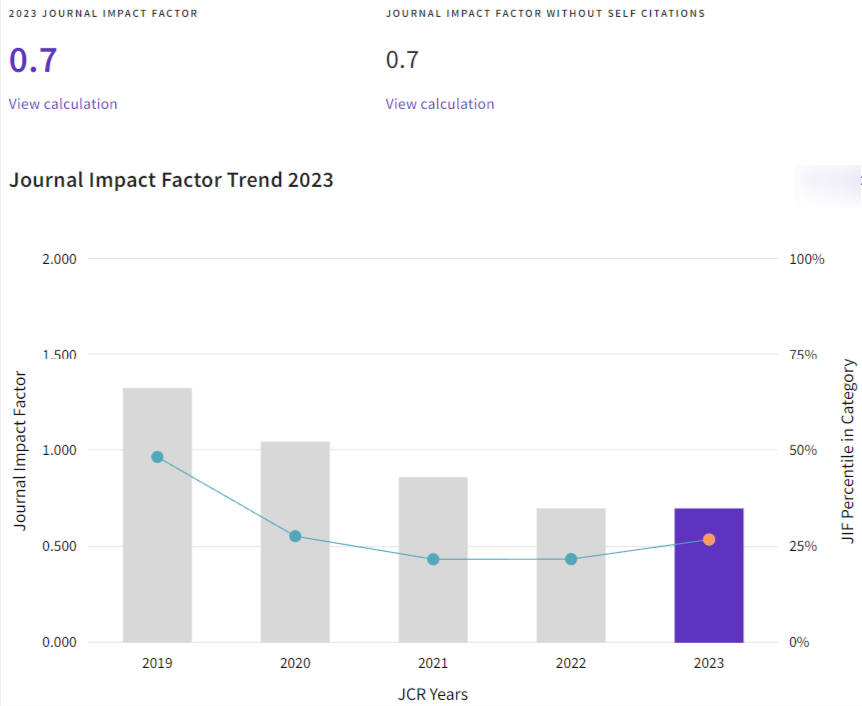
2023 = 0.7
Índice SCIMAGO
Scopus CiteScore
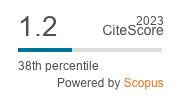


2023 = 0.7

REVISTA MEXICANA DE CIENCIAS PECUARIAS Volumen 16 Numero 1, Enero-Marzo 2025. Es una publicación trimestral de acceso abierto, revisada por pares y arbitrada, editada por el Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (INIFAP). Avenida Progreso No. 5, Barrio de Santa Catarina, Alcaldía Coyoacán, C.P. 04010, Cuidad de México, https://www.gob.mx/inifap.
Distribuida por el Centro de Investigación Regional Sureste, Calle 6 No. 398 X 13, Avenida Correa Racho, Col. Díaz Ordaz, Mérida Yucatán, C.P. 97130.
Editor responsable: Arturo García Fraustro Reservas de Derechos al Uso Exclusivo número 04-2022-033116571100-102, ISSN: 2448-6698, otorgados por el Instituto Nacional del Derecho de Autor (INDAUTOR).
Responsable de la última actualización de este número: Arturo García Fraustro, Campo Experimental Mocochá, Km. 25 Antigua Carretera Mérida–Motul, Mocochá, Yuc. C.P. 97454. http://cienciaspecuarias. inifap.gob.mx, la presente publicación tuvo su última actualización en febrero de 2025.